|
Introduction
The "sky map" that you have plotted shows the motion of the Sun and Mercury in right ascension and declination. This shows their motion relative to the background of the stars, which are fixed in position. To see their relative positions, it is easier to use a different set of coordinates, celestial latitude and celestial longitude.
Celestial latitude and longitude are measured in a way similar to latitude and longitude on the Earth, using the Ecliptic in place of the Equator. We can draw circles parallel to the Ecliptic, which are called parallels of celestial latitude, and perpendicular to the Ecliptic (through the North and South Ecliptic Poles), which are called meridians of celestial longitude. The celestial latitude of an object is the distance between it and the Ecliptic, measured along the meridian of celestial longitude that goes through the object. The celestial longitude is the distance between the Vernal Equinox and the meridian of longitude through the object (always) measured eastwards along the Ecliptic.
The latitude of the Sun is always zero, since we use its motion to define the Ecliptic. Its longitude is zero on the first day of spring, and increases by 360 degrees in one year, or about 1 degree per day. The table of Solar Celestial Longitudes which you have gives the longitudes of the Sun every 4 days; you can see that the difference between the numbers is always around 4 degrees, corresponding to the average motion of 1 degree/day, multiplied by the 4 day interval.
The latitude and longitude of Mercury are continually changing. A glance at the graph from part 1 shows that Mercury's path crosses the Sun's path in a number of places, so that it is sometimes north of the Sun, and sometimes South; this means that its latitude must be continually changing. Your sky map also shows that Mercury is normally moving eastwards along the Ecliptic, but that it occasionally turns back to the west, in some sort of looping or arcing motion. We call the normal eastward motion DIRECT motion, and the (occasional) westwards motion RETROGRADE motion, so these loops and "esses" are called retrograde loops or esses.
Measuring the Sky Map
To measure the latitudes and longitudes of Mercury, cut a corner about 1.5 to 2 inches square from a stiff piece of paper (such as an index card), and mark the edges in degrees by lining it up with the 10-square to the inch graph paper you used for your Mercury graph. (You could also just cut out a squared-off piece of the graph paper, but aside from the difficulty of cutting it exactly midway on one of the accented lines, the graph paper is relatively thin and tends to curl, particularly after having been handled a while, making measurements more difficult. A stiffer piece of paper tends to lie flatter, making it easier to work with.) Counting the corner as 0 degrees, mark whole degrees in both directions from the corner, so you can measure along either edge of the paper. Be sure to use the same scale as on the original graph, 5 degrees per inch, with each tenth-inch square being 1/2 degree, and mark 5 degrees in each direction from the corner (you can mark it further than 5 degrees if you want, but you'll never need to measure even that far).
Lay the measuring paper on your Mercury graph and move it along the Ecliptic, so that the "zero" corner is exactly on the Ecliptic and one side is exactly perpendicular (at right angles) to the Ecliptic, until the perpendicular side exactly lines up with one of the dots for Mercury. Then the longitude of Mercury can be estimated from the numbers along the Ecliptic side of the piece, and the latitude from the numbers along the perpendicular side. Note that since the Ecliptic gradually curves, and the edge of the graph paper is straight, the side of your measuring paper that is more or less "on" the Ecliptic will lie exactly on it only at the corner, as the Ecliptic gradually curves away from or toward it.
The distance north or south of the ecliptic, measured along the perpendicular edge, is the celestial latitude of Mercury. The celestial longitude is found by measuring the distance from the corner of the paper to the NEAREST dot for the Sun, and adding that value to (or subtracting that value from) the longitude of the Sun's dot (which should be right next to it, if you've labeled the map correctly, as described at the end of part 1). If Mercury's position is to the east of the Sun, so that its right ascension is larger, then its longitude is also larger and you need to add the difference; if Mercury is to the west of the Sun then its longitude is smaller, and you need to subtract the difference. In any case, you can see which way the numbers should go by looking at the solar positions that lie on either side of Mercury; and AFTER you do the addition or subtraction, make sure you did it right by comparing Mercury's longitude to the longitudes of the solar dots on either side of it. Mercury's longitude MUST be in between the solar values; if it does not, you have added where you should have subtracted, or vice-versa.
(Example 1, Figure 1: Mercury to West of nearest Solar dot)
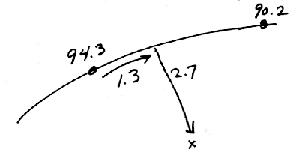
In Figure 1, Mercury is 2.7 degrees south of the Ecliptic, and 1.3 degrees west of the nearest dot for the Sun (at 94.3 degrees longitude, according to the number next to it). The celestial latitude is therefore 2.7 South, exactly the same as the measured distance; and the celestial longitude is 93.0 degrees, which is the longitude of the Sun's dot, 94.3, MINUS (since the numbers get bigger to the East) the 1.3 degree difference in position. Note that the value of 93.0 is reasonable, since Mercury lies between longitude 94.3, the position of the solar dot to its east, and longitude 90.2, the position of the solar dot to its west; if you had added the 1.3 degrees to 94.3, you would have gotten 95.6, which is obviously incorrect.
(Example 2, Figure 2: Mercury to East of nearest Solar dot)
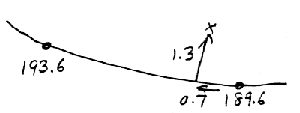
In Figure 2, Mercury is 1.3 degrees north of the Ecliptic, and 0.7 degrees east of the nearest dot for the Sun (at 189.6 degrees longitude, according to the number next to it). The celestial latitude is therefore 1.3 North, exactly the same as the measured distance; and the celestial longitude is 190.3 degrees, which is the longitude of the Sun's dot, 189.6, PLUS (since the numbers get bigger to the East) the 0.7 degree difference in position. Note that the value of 190.3 is reasonable, since Mercury lies between longitude 193.6, the position of the solar dot to its east, and longitude 189.6, the position of the solar dot to its west; if you had incorrectly subtracted the 0.7 degrees from 189.6, you would have gotten 188.9, which is obviously wrong, because it doesn't lie between the two solar values.
(Example 3, Figure 3: Mercury below and to left of nearest Solar dot)
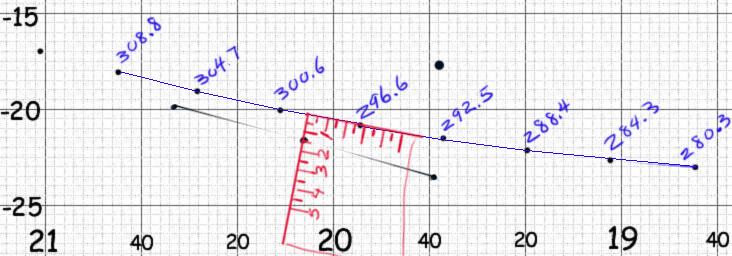
In figure 3, we see an example in which the actual dots for the Sun, as shown in part 1, and some not-quite-correct dots for Mercury are compared, using the corner of an imaginary "piece of paper", marked in degrees and tenths of degrees, to show how the measurements are done. One side of the measuring paper is placed perpendicular to the Ecliptic, so that the corner is exactly on the Ecliptic, and the other side of the measuring paper is more or less along the Ecliptic, heading toward the nearest dot for the Sun. The distance perpendicular to the Ecliptic (about 1.5 degrees, as shown) is Mercury's celestial latitude, written as minus or South (since it is below the Ecliptic) 1.5 degrees. The distance from the corner to the nearest Solar dot (about 2.8 degrees, as shown) is added to the longitude of that Solar dot (296.6 + 2.8 = 299.4 degrees, in this case), to obtain Mercury's longitude. Note that as shown, the Solar dot used for comparison is NOT the nearest Solar dot. You should ALWAYS use the NEAREST Solar dot for this comparison. The further dot is used, as in this case, only when the nearest dot is at least 1.5 degrees away, and you need to measure both ways, and take an average (see the discussion below these illustrations).
(Example 4, Figure 4: Mercury above and to left of nearest Solar dot)
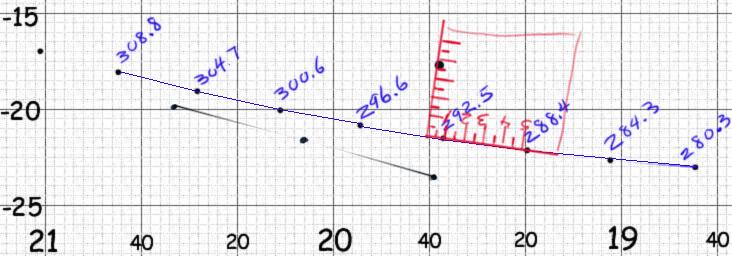
In figure 4, we have another (faked) example of a dot for Mercury, measured with an imaginary piece of paper, relative to the actual dots for the Sun. Again, the measuring paper is aligned so that one side runs right through the dot for Mercury, and is perpendicular to the Ecliptic, the corner is exactly on the Ecliptic, and the other side of the measuring paper is more or less aligned with the Ecliptic. In this illustration, the latitude is shown as plus or North (since the dot is above the Ecliptic) 3.7 degrees celestial latitude, and the longitude is shown as the longitude of the Solar dot used for comparison, plus the distance along the Ecliptic to the corner of the paper, because the measurement is being done in the direction of larger longitudes (as was also true for Example 3), or 292.5 + 0.9 = 293.4 degrees celestial longitude. Note that the dot for the Sun labeled 292.5 would also be used to measure the first dot for Mercury, which is below the Ecliptic. Some Solar dots will be used to measure the positions of three or four Mercury dots, while other Solar dots may not be used to measure the position of any dots for Mercury. Still, every Solar dot has to be labeled with its position, so that if it is needed, the longitude is right next to the dot, when you need it.
If your sky map were a perfect representation of the sky, then it would not have made any difference which solar dot you compared to Mercury; but it is not. The vertical lines on your graph paper represent hour circles, which must all come together at the Poles, and which must therefore gradually get closer and closer together as they get further and further from the Equator. But of course this is not the way the graph paper is printed; the vertical lines are the same distance apart everywhere, so at high declinations (far from the Equator) they are TOO FAR APART. As a result, depending upon the declination, there is a map distortion which can increase your measured longitude differences by almost 10%. If your longitude differences are small, as in the above examples, any errors must be small (only about 0.1 degrees). But if, by accident, the meridian through Mercury fell about halfway between the nearest two solar dots, then map distortion errors could be as much as 0.2 degrees.
To avoid problems with map distortion, you should ALWAYS measure the distance to the NEAREST solar dot, so that any map distortion error is as small as possible. If that distance is less than 1.5 degrees, then map distortion errors can't be more than 0.1 degrees, so you can use the longitude measured in this way. But if the distance is 1.5 degrees or more, map distortion errors may be more significant. To make sure that this is not the case, you should then measure the longitude difference to the solar positions on BOTH sides of Mercury's meridian, and calculate the longitude from each of the two differences. Near the Equator, the two values should be about the same, but as we approach the Solstices, they will begin to diverge; the value measured relative to the western solar dot (where you are adding the difference) will be too large, and the value measured relative to the eastern solar dot (where you are subtracting the difference) will be too small. In this case, you should average the two longitude values for best results.
Finding the Position of Mercury Relative to the Sun
Unfortunately, what we need for the final part of the project is not the position of Mercury relative to the Ecliptic and the Vernal Equinox (which is what the latitudes and longitudes give us), but its position relative to the Sun. So we need to compare the position of Mercury on each date to the position of the Sun, by subtracting the Sun's position from that of Mercury. Since the Sun is always on the Ecliptic, its latitude is always zero, so the number for Mercury's latitude is the required difference. For the longitude, however, you need to subtract the Sun's longitude on a given day (which is normally NOT the same as the longitude of the Solar dot you used to measure Mercury's position) from Mercury's longitude on the SAME day. This difference in longitude is called the ELONGATION of Mercury.
To organize your results, make a table similar to the one here (note that, although the numbers shown here are similar to the ones you will obtain, they are just made up, and are NOT numbers you should try to match). You can enter all 135 dates, and the corresponding Solar longitudes (the same numbers you used to label the Solar dots) before you even make any measurements of latitude or longitude. After you make the measurements and enter the latitude and longitude into the table, you can subtract the Sun's position, as discussed above, to get the Elongation of Mercury. If Mercury's longitude is larger than that of the Sun, then Mercury is at an EAST elongation. If the Sun's longitude is larger, then Mercury is at a WEST elongation. Be sure to label each elongation as being East or West, and label each latitude as being North or South, as you do the measurements and calculations.
Mercury's Longitude - Sun's Longitude = Mercury's Elongation |
| Date | Mercury's Latitude | Mercury's Longitude | Sun's Longitude | Mercury's Elongation |
| 4970 | South 2.1 | 292.5 + 0.2 = 292.7 | 280.3 | 12.4 East |
| 4974 | South 2.0 |
296.6 + 2.0 = 298.6
300.6 - 2.2 = 298.4 | (average=298.5)
|
284.3 | 14.2 East | |
| 4978 | South 1.7 | 304.7 + 0.5 = 305.2 | 288.4 | 16.8 East |
| 4982 | South 1.2 | | 292.5 | |
| 4986 | South 0.5 | | 296.6 | |
| 4990 | North 0.7 | | 300.6 | |
An Apparently Odd Situation
At the beginning of Spring the Sun passes the Vernal Equinox (this is how the beginning of spring is defined), and when it does its celestial longitude, which had been steadily increasing towards 360 degrees, suddenly drops to zero. Since Mercury is always close to the Sun, it will do this at about the same time, but since it may be as much as 27 degrees ahead of or behind the Sun, it may do it earlier or later than the Sun does, producing what appears to be a very strange situation, but is simply an arithmetical quirk.
Before either of the two bodies reaches the Vernal Equinox, and after both of them have done so, the numerical value of Mercury's elongation, as calculated from the formula in the table above, will be less than 27 degrees. But during the time when one of them has already passed the Vernal Equinox, and the other one has not yet reached it, the one that has passed the Equinox will have a celestial longitude close to zero, and the one that has not yet reached it will have a celestial longitude close to 360 degrees. If, in such a case, you subtract one longitude from the other in the usual way, you will obtain an elongation close to 360 degrees, which looks completely out of place in the normal progression of results.
There isn't actually anything wrong with such an answer. It is just an unexpected way of stating the elongation, more or less the same as saying that Santa Ana is almost 360 degrees west of Long Beach. That is perfectly true, but we would normally say that it is less than one degree to the east of Long Beach. We use the direction that provides a smaller, easier to visualize answer. So if Mercury's elongation comes out as, say, 353 degrees west of the Sun, that just means that it is 7 degrees east of the Sun, and the Equinoctial passage just happened to cause an answer in the "wrong" direction.
To adjust for this situation, simply do as follows: if the elongation is more than 180 degrees, subtract it from 360 degrees, and reverse the direction (e.g., in the example just stated, 353 west is subtracted from 360, yielding 7 east).
Next: Parts 2b and 2c
|