The Search for Proof That the Earth Moves
Prior to the Copernican revolution the Earth was presumed to be fixed in place, neither rotating on its axis nor revolving around the Sun. The daily westward motion of the stars caused by our rotation was thought to be a real motion of the Celestial Sphere around the Earth; and the annual eastward motion of the Sun caused by our orbital motion was thought to be an orbital motion of the Sun around the Earth. But if Copernicus was correct in putting the Sun in the center of the Solar System, then the Earth must be moving, and there are presumably effects caused by its motion that we ought to be able to see.
This had been realized even in ancient times, in discussions about the rotation of the Earth (though as is the case today, these were often more heated arguments than reasoned discussions). The general feeling was that the Earth could not move, because if it did (1) we would feel a strong wind blowing in the opposite direction to our motion, due to the difference between the motion of the air and the Earth; and (2) things thrown upwards would fall to the west of their expected position, because of the eastward motion of the Earth underneath them, while they were in flight.
In modern thinking (Galilean relativity, to be specific), such effects are
not expected, because at any given time everything which is at rest relative to us is moving eastward with us, while we rotate, at the same rate that we are; and any motion that we might observe things to have if we were at rest would appear the same even if we were moving, insofar as our motion is uniform.
But if we can't observe the effects of our motion directly, how are we to tell whether we are moving at all?
Very early on, it was realized that if the Earth moved around the Sun the positions of the stars would change, due to
stellar parallax. And in fact, many observers in the late 1500's claimed to have actually observed such changes; but the much more accurate observations of
Tycho Brahe showed that there was no change in stellar positions which could be attributed to anything other than observational errors; and given the lack of any reliable observations of stellar parallax, Tycho rejected the idea that the Earth moved. The exact reason he did so isn't entirely clear (though it may have had to do with erroneous interpretations of the apparent size of stars of different brightness), but we can be certain that if he
had observed stellar parallax, he would have adopted the Copernican view of things.
We "Know" Copernicus Was Right; But Can We Prove It?
By the early 1600's Galileo's thought and physical experiments on the nature of motion and his astronomical observations had led him to the basic premise of Galilean relativity: the laws of nature should appear the same no matter how you are moving. Whatever you can hope to observe when at rest should appear the same in terms of the laws of nature if you are moving (though the actual observations might need some minor corrections caused by non-uniform motions). In other words, ancient objections that if we moved we would see various effects caused by that movement (which we do not see) are incorrect. In general, things should look the same whether (as in the case of students in my classroom at LBCC) we are moving to the east at 850 miles per hour, or we are at rest.
In the about the same era (though concluding a bit earlier) Kepler showed that the motions of the planets could be far more easily and elegantly explained as being due to elliptical motions around the Sun, rather than some complex combination of circular motions around the Earth; and the result of the combination of Galileo's principles of motion and Kepler's analysis of planetary motions was that most natural philosophers (that is, scientists) of the early to mid 1600's came to accept the reality of the Earth's motion without any observational proof that it did move. But that didn't affect the desire to
observe the effects of that motion, and in some ways made that desire even stronger, for it is unsettling to believe in a scientific theory without any observational proof to support it.
Unfortunately, the parallactic movement of stars caused by our orbital motion around the Sun is incredibly small (smaller, even, than the size of the smallest stellar images on every photograph of the sky taken more than a few years ago), and the technology required to observe that motion would not be achieved until the 1800's. So for over two hundred years, astronomers and other scientists might have believed the Copernican theory without any observational proof that it was correct; but during that interval the fact that stellar parallax was so incredibly small (meaning that the stars are so incredibly far away) wasn't known, and it was always hoped that "any day now" more accurate observations would provide the evidence needed to prove that we are moving. And so the search went on and on.
By the late 1600's it had been shown that Polaris, whose altitude is relatively constant on account of its position near the North Celestial Pole, and as a result is a little easier to accurately measure than for stars whose altitudes change dramatically (which required corrections due to atmospheric refraction that were much larger than the quantities being measured; meaning that any error in those corrections could destroy the evidence being looked for), changed its position in a regular manner by 40 seconds of arc (40") each year. Unfortunately, the direction of the change was not what one would have expected if it were caused by stellar parallax, so additional observations of other stars were attempted, to clarify the matter.
Bradley's Efforts to Observe Stellar Parallax
The star of greatest importance at this point in the story is γ (gamma) Draconis, also known as Eltanin, or Etamin (it is this sort of confusion in common names that led Bayer to adopt Greek letters for enumerating the stars), which was soon found to have an alteration in its position similar to that of Polaris. (The reason Eltanin/Etamin was chosen for this purpose is that it passes nearly overhead in London, and by observing it as it passed near the zenith on different dates the effects of atmospheric refraction, which are zero at the zenith, could be ignored.)
In 1725 James Bradley, who held a position at Oxford as astronomer and natural philosopher, began observations of γ Draconis at the home of a friend, Samuel Molyneux. Using a telescope attached to a chimney so that it pointed nearly vertically, he changed the position of the telescope very slightly, and very accurately measured its change in position using a screw and plumb-line; and over the course of a year or so found that the star did indeed vary in position during the course of the year by 40 arc-seconds, just like Polaris. But, exactly like Polaris, the change in motion was in the wrong direction for stellar parallax, as shown in the following diagram:
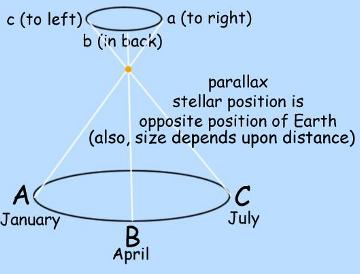 
How Bradley's observations differed from the expected effects of parallax. As shown on the left, as the Earth moves to one side of its orbit, γ Draconis should move to the opposite side of its parallactic ellipse (the path the star seems to follow during the year as a result of our motion around the Sun). Thus, when the Earth is at points A, B and C, the star should appear to be at points a, b and c. Instead, as shown on the right, as the Earth moves from one point to the next the apparent positions are shifted in the direction of the Earth's motion, which is a quarter circle ahead of the expected parallactic shift. In addition (although not demonstrated here), the amount of the parallactic shift should depend upon the star's distance, being larger for closer stars and smaller for more distant stars; whereas the so-called stellar aberration observed by Bradley is the same for every star in a given region, regardless of its distance. (Parallax produces an elliptical motion, circular at the Ecliptic poles and linear at the Ecliptic plane, whose semi-major axis equals the reciprocal of each star's distance in parsecs, which is of course different for different stars. Stellar aberration produces an elliptical motion, circular at the Ecliptic poles, and linear at the Ecliptic plane, whose semi-major axis equals a constant regardless of the distance or angular position of the star, that constant being equal to one radian multiplied by the ratio of the Earth's orbital velocity to the speed of light. Said statements to be explained in later revisions of this page.) |
A Fortuitous Discovery
Confronted by observations which made no sense in terms of the Earth's supposed motion, Bradley decided to make additional observations, first of other stars that passed very nearly overhead, then, by improving the mount of the telescope so that it could be just as accurately aligned over an angle of more than three degrees from the vertical, still other stars. But no matter which stars he observed the annual motion presumably produced by the Earth's motion around the Sun was always in the wrong direction, and always the same size, despite the probably different distances of the stars involved. What in the world could possibly be the cause of this inexplicable result?
One possibility was that the axis of the Earth did not maintain a constant position in space, or even move (causing the precession of the Equinoxes) around the pole of the Earth's orbit, as shown by Copernicus, at a constant rate; but had an additional annual motion -- a sort of "nodding", or nutation -- that made the stars merely seem to change their positions, because those positions were being measured relative to the (changing) position of the Earth's axis of rotation. And in fact, nearly twenty years later, after a careful study of the motions of the stars during the 18-year cycle of lunar orbital changes, Bradley announced that there was indeed a nutation of the Earth's axis, related to the motion of the Moon. However, this was
not the cause of the annual changes in stellar position, and a completely different explanation was required.
As often happens in science (recall Newton's "discovery" of the nature of gravity when an apple fell to the ground while he was in his orchard), the answer came from a completely unscientific pursuit. While sailing on the Thames Bradley noticed that as he turned the boat the direction of a vane on the mast changed, and being aware that the change was not due to a change in the wind, but in the direction of the boat, he realized that the puzzling change in the direction of the stars might be caused not by the
changing position of the Earth, but by the its
changing motion.
To understand this, consider the diagram below:
 The "aberration" of rain and light "falling" toward a moving observer. On the left an observer is running in the rain. The moving observer will not see the rain falling from its true direction, but at an angle to that direction determined by his speed divided by the rain's speed, and the angle of his motion relative to the rain's actual motion (shown here as being vertical, and therefore perpendicular to his motion). The faster he goes the more nearly the rain will appear to fall horizontally; the slower he goes, the more nearly it will appear to fall vertically. Similarly, as shown on the right, a beam of light from a distant star will appear to be coming from a little "in front" of its true position because of the motion of the Earth, at an angle to its true position determined by the Earth's speed, divided by the speed of light, times the sine of the angle between the direction to the star and the direction of the Earth's motion. Since the Earth's orbital velocity is one ten-thousandth (1/10,000) of the speed of light, the star's position changes by up to one ten-thousandth of a radian (360 degrees divided by 2π, divided by 10,000), or approximately 20 seconds of arc whether the star is near the Ecliptic Pole, or in the plane of the Ecliptic, but at right angles to the Earth's current direction of motion. |
Now let's use another diagram, to apply this to the orbit of the Earth:

The change in stellar position (stellar aberration) caused by the Earth's velocity of motion around the Sun. In the diagrams on the left, the Earth is shown at point A, moving in the direction of the arrow. This produces a change in the position of the star relative to its "correct" position, shown by the arrow going from the star's average position, to point b. In the diagrams on the right, the Earth is shown at point B, moving in the direction of the arrow shown there. This produces the change in position shown by the arrow going from the star's average position, to point c. Thus the change in position (stellar aberration) caused by the Earth's velocity is three months ahead of the change expected for a stellar parallax produced by a change in the position, which is exactly what Bradley had observed. |
The Earth Does Move, After All
Now one thing of great importance should be stressed. Stellar aberration, produced by the direction of motion of the Earth (and as shown below the speed that it has compared to the speed of light) is different from stellar parallax, produced by the change in position of the Earth (which depends upon the size of our orbit, compared to the distance of the star); but
it is still produced by our motion. In other words, although what Bradley discovered was
not the stellar parallax he and others had been looking for during the previous century and a half,
it was irrefutable proof that the Earth does move. In fact, it is also a measure of how fast the Earth moves, because the size of the aberration is a direct observation of a particular ratio, namely the speed of the Earth compared to the speed of light. For in the diagrams showing how the direction of falling rain or "falling" light would be altered by an observer's motion, the size of the angular change in direction is directly related to the ratio of the speed. Without going into the geometrical details,