|
(Slightly updated Feb 7, 2015, primarily to fix problems with non-standard symbols)
The Mass-Luminosity Diagram
Stars have a huge range of luminosities, from red dwarfs 50,000 times fainter than the Sun to supergiants 1,000,000 times brighter than the Sun. They also have a large range of mass, from red dwarfs over 10 times less massive than the Sun to blue giants 100 times more massive than the Sun.
For a given star such as the Sun, the brightness can change considerably during its lifetime. While the Sun and planets were forming the Sun was probably 100 to 200 times brighter than now. During the first billion years of its Main-Sequence lifetime it was probably only about 2/3 as bright as now. Towards the end of its Main-Sequence lifetime it will be over 50% brighter than now, and as it swells up to become a red giant it will become larger than the orbit of the Earth and over 1000 times brighter than now. After it ends its Red Giant phase it will shrink to become a white dwarf, 1000 to 10000 times fainter than now.

Hertzsprung-Russell Diagram Showing The Sun's Evolutionary Path
and Brightness at Different Stages of its Evolution
Since the brightness of the Sun changes during its lifetime, if we tried to compare its brightness to its mass we would get different results at different times. Because of this we cannot get any useful relationship between stars' masses and luminosities unless we restrict ourselves to special circumstances.
One such circumstance is if we restrict ourselves to Main-Sequence stars. Since the characteristics of a Main-Sequence star are almost constant for long periods of time, we don't need to worry about changes in the brightness altering the results of a comparison such as the one shown in the next figure:
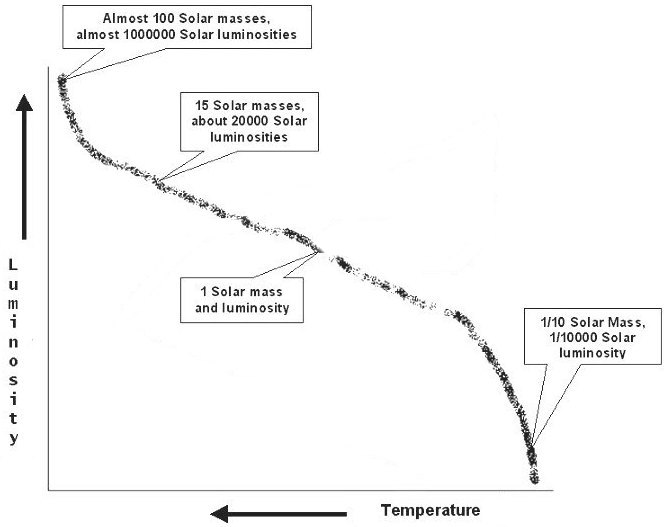
Hertzsprung-Russell Diagram Showing Masses and Luminosities of Main Sequence Stars
As this figure shows, the stars at the top of the Main Sequence are very massive, the ones in the middle have average mass, and the ones at the bottom have very little mass.
We can show the relationship of mass and luminosity more clearly by plotting a Mass-Luminosity Diagram for Main-Sequence stars:
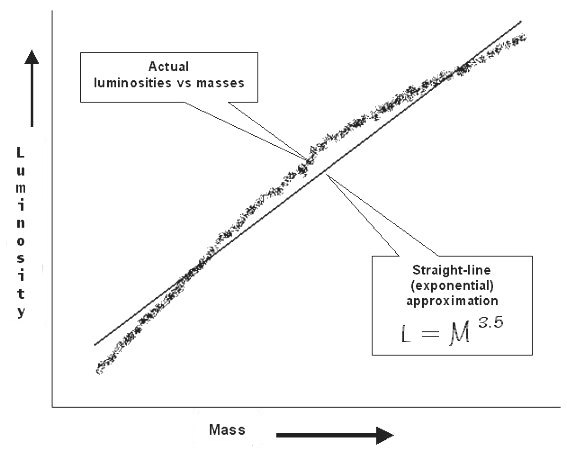
Mass-Luminosity Diagram
As shown in the diagram, the masses and luminosities of Main-Sequence stars steadily increase in tandem, though not in a perfectly uniform way. The curve represents the actual relationship between mass and luminosity; the straight line represents a simple approximation to the actual relationship. (For those who are mathematically inclined, the curve may look pretty simple too. But keep in mind that the range of luminosity shown here is over 10 billion times, and the range of mass is about 1000 times. To show the results of such a huge range of numbers in such a compact graph requires the use of log-log coordinate paper. On such a graph even a straight line represents an exponential equation, and curved lines represent very complex relationships.)
The relationship between mass and luminosity shown on the above graph is so important to our understanding of the characteristics of Main-Sequence stars that it is given a special name. If we represent it by a graph we call it the Mass-Luminosity Diagram. If we represent it by an equation we call it the Mass-Luminosity Relationship (shown in the above diagram as a straight-line approximation, with Luminosity approximately proportional to an exponential power of the Mass).
The Mass-Luminosity Relationship
As shown in the graph above, the brightness of Main-Sequence stars varies proportional to some power of their masses. For most of the range of stellar masses the proportionality is as the 3.5 power of the mass, which means that if the mass doubles, the luminosity increases by about 11 times, or rounding off a bit, about 10 times. As a result, we can estimate the brightnesses of various stars by doubling (or halving) the mass, and multiplying (or dividing) the luminosity by 10. The table below shows how this works:
Stars More Massive Than the Sun
1 solar mass has 1 solar luminosity (L☉)
2 solar mass stars have 10 L☉
4 solar mass stars have 100 L☉
8 solar mass stars have 1000 L☉
16 solar mass stars have 10000 L☉
32 solar mass stars have 100000 L☉
64 solar mass stars have 1000000 L☉
| Stars Less Massive Than the Sun
1 solar mass has 1 L☉
1/2 solar mass stars have 1/10 L☉
1/4 solar mass stars have 1/100 L☉
1/8 solar mass stars have 1/1000 L☉
1/16 solar mass stars have 1/10000 L☉
|
At the high end of the mass scale the brightness changes more slowly than shown here, and a 1000000 solar luminosity Main Sequence star would actually be about 100 solar masses instead of 64 solar masses, but considering that the range of brightness here is 10000 million times and the range of mass about 1000 times, it is remarkable that such a simple calculation is so nearly accurate.
The Main-Sequence Lifetime of Stars
The relationship between brightness and mass has serious implications for the lifetimes of the Main Sequence stars. The fuel that keeps stars shining is their mass (or more specifically, the mass of hydrogen in the core of the star), and stars that have more mass have more fuel to burn, so you might expect them to last longer than stars with less mass. But the rate at which the fuel has to be burnt is proportional to luminosity, so brighter stars shouldn't last as long as fainter ones. The ratio of a star's lifetime to the lifetime of the Sun would be given by how much more fuel it has, divided by how much faster it is burning that fuel. Since for most of the range of stellar masses Main Sequence stars which are twice as bright are burning their fuel ten times faster (twice the mass producing ten times the luminosity as shown above), their fuel will only last about one-fifth (2/10) as long. As a result, we can modify the table shown above to include the lifetimes of the stars. (Note: In this table the lifetimes are rounded off, since the luminosities shown above are only approximately correct. Even the Sun's Main Sequence lifetime, which is around 12 billion years, is rounded off to 10 billion years, to keep the numbers simple. Also, for those not in the United States, remember that on this site a billion is only a thousand million, and a trillion is only a million million.)
Stars More Massive Than the Sun
1 solar mass has 1 solar luminosity (L☉) and lasts about 10 billion years
2 solar mass stars have 10 L☉ and last about 2 billion years
4 solar mass stars have 100 L☉ and last about 400 million years
8 solar mass stars have 1000 L☉ and last about 80 million years
16 solar mass stars have 10000 L☉ and last about 15 million years
32 solar mass stars have 100000 L☉ and last about 3 million years
64 solar mass stars have 1000000 L☉ and last less than a million years
| Stars Less Massive Than the Sun
1 solar mass has 1 L☉ and last about 10 billion years
1/2 solar mass stars have 1/10 L☉ and last about 50 billion years
1/4 solar mass stars have 1/100 L☉ and last about 250 billion years*
1/8 solar mass stars have 1/1000 L☉ and last more than a trillion years*
1/16 solar mass stars have 1/10000 L☉ and would last more than 5 trillion years*
(* see text below for stars of 1/4 solar mass or less) |
Since the luminosities shown here are only approximate, the lifetimes would be only approximate even if there were no other complications, but for the lowest mass stars there is an additional complication. The lifetimes of stars like the Sun and higher mass stars are as "short" as they are because only the fuel in their cores is burned while they are on the Main Sequence. If the Sun could burn all of its fuel throughout its entire mass at the current rate it could actually last about 100 billion years. It only lasts about 10 billion years because only the central part of the Sun is hot enough to support nuclear fusion. The same is true of all the stars, and so in all of them the fuel is being "burnt" only in the center. But for stars whose evolutionary path moves more or less straight down to the Main Sequence during their formation, the convective zone (or convective envelope) on the outside of the star reaches deep into the core of the star, and as the fuel in the core is used up fresh fuel is cycled into the core from the outside. As a result those stars do burn all of the fuel throughout the star while they are Main Sequence stars, even though the actual burning takes place only in the center. This increases the lifetimes of 1/4 and 1/8 solar mass stars by about another factor of 8, to about 2 trillion years and 10 trillion years, respectively. The 1/16 solar mass stars would last even longer, but as discussed on the pages about stellar death, stars of that low a mass probably never get hot enough to support nuclear burning, so they don't have any Main Sequence lifetime at all.
Now what does this mean? If massive stars don't last very long, then any bright massive stars which we see must have been "born" (formed) relatively recently. In fact the most massive stars must have been born yesterday, by astronomical standards. Even the least massive stars shown in the table of stars more massive than the Sun, stars with two Solar masses, have lifetimes less than half the age of the Solar System. This means that if the Sun were still in the cluster of stars that it formed in, it would be one of the brightest stars in that cluster. All the stars that were originally brighter than it, from just a little brighter to a million times brighter, would already be dead. Their dead hulks would still be around, but they would be either unobservably faint or just barely bright enough to see with large telescopes.
On the other hand, the stars which are lower in mass than the Sun have much, much longer lives than the Sun. In fact, although stars like the Sun, if formed early in the history of the Universe (sometime between 12 and 15 billion years ago) would already be dead, every single star with around half or less the mass of the Sun that has ever been formed would still be shining just as brightly (or perhaps we should say just as faintly) as ever, because their lifetimes are all much longer than the age of the Universe.
Why Bright Stars Are Rare
Even when star clusters first form, the bright stars are not as numerous as the fainter ones because the brighter ones require more mass, and even if 90% of the mass of the cluster were in the brightest stars, you wouldn't get all that many of them since each one uses up so much mass, while the 10% or so of mass that formed into low mass stars could become a great many stars because each of them doesn't require much mass. But in addition the bright stars die out very quickly, so after a while their number drops to zero, while the faint stars last practically forever, and their number remains as large as when they first formed.
|