|
Black Body Radiation and Stellar Spectra
"Black body" radiation is the light (including invisible forms of electromagnetic radiation) given off by a "perfect" or "ideal" radiator. In general, the better things are at absorbing light the better they are at emitting it, so a perfect absorber should be the most efficient radiator possible; but if something is a perfect absorber it will not reflect any radiation, and will look black. Hence the strange name of the radiation given off by a perfect radiator.
Since stars have no surface in the ordinary sense of the term, any radiation that enters a star is very likely to be scattered and absorbed until it is completely lost, making stars very close to perfectly black bodies as far as absorption is concerned; and as a result it would be reasonable to suppose that they would be perfect, or black body radiators as well.
However, at their apparent surfaces stars are not actually perfect radiators, because the absorption of light at individual wavelengths by various atoms and ions blocks part of the outward flow of radiation, and this has to be made up for by emitting more light at other wavelengths (the radiation that is blocked heats up the gas, causing it to emit enough extra light at unabsorbed wavelengths to make up for the line absorptions). As an example the spectrum of the Sun is shown in red below, in comparison with the spectrum of a black-body of 5780 Kelvins, shown in orange. By and large the spectra are the same, but the absorption of light at various wavelengths (where the red spectrum of the Sun dips below the orange spectrum of a black body with the same temperature as the "surface" of the Sun) is balanced by an excess of light at other wavelengths (where the red spectrum of the Sun lies above the orange spectrum of the black body).
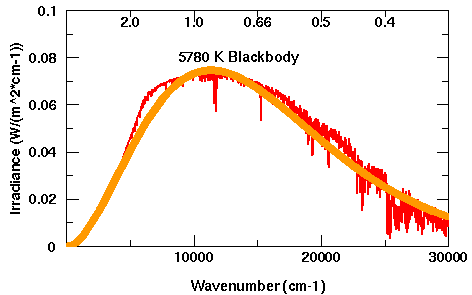
A comparison of the radiation of the Sun with a "black-body" radiator of the same temperature
Black Body Radiation Laws
The diagrams and equations below summarize the appearance of black body spectra of various temperatures, and the relationship between the temperature of a black body radiator and the color and intensity of its radiation.
 A "log-log" plot of black body radiation curves. Wavelength increases from left to right, while brightness per square foot increases upwards. Each horizontal line represents 10 billion times more radiation than the one below it. The vertical lines represent the range of visible light from violet (on the left) to red (on the right). The curves, from lowest to highest, represent temperatures of 3000, 6000, 12000, 24000 and 15 million (the approximate value for the center of the Sun) Kelvins. In this sort of plot the shape of each curve is identical, but hotter bodies radiate far more light, especially at shorter wavelengths.
 Closeup of black body radiation curves for wavelengths near those of visible light. Wavelength increases from left to right, while brightness per square foot increases upwards. The top of the graph represents one thousand times more light than the bottom. The vertical lines represent the range of visible light from blue and violet (on the left) to red (on the right). The curves, from lowest to highest, represent temperatures of 3000, 5780 (the value for the Sun), 12000 and 24000 Kelvins. Cooler bodies radiate more in the red and infrared, and hotter bodies in the violet and ultraviolet.
Wien's Law:
The wavelength of maximum brightness is inversely proportional to the gas temperature
or wmax = (a conversion constant) / T
Stefan's Law:
The brightness per square foot is proportional to the fourth power of the gas temperature
or B / (square feet) = (a conversion constant) x T4
|