The orbits of the planets are ellipses, with the Sun at one focus of the ellipse.
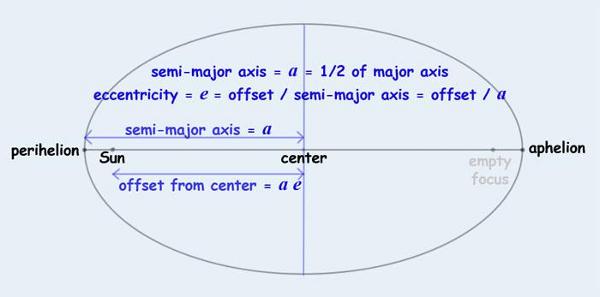
The size of the orbit is defined as the average distance from the Sun, or more specifically the average of the perihelion and aphelion distances, which -- since those points are at opposite ends of the major axis -- is the semi-major axis, symbolized mathematically by the letter a.
The shape of the orbit is defined by its ellipticity, which is the difference between the length of its minor axis and the length of its major axis, expressed as a fraction of the major axis; but this is significant only when the ellipse has some kind of physical reality, as in the ellipsoidal profile of a rapidly rotating planet.
Since the ellipses used to describe planetary orbits are mathematical fictions which have no physical reality, their shape is of little importance; but the position of the Sun within an orbit is important, as it defines how much closer or further the planet can be at perihelion or aphelion than on the average. This is expressed by the eccentricity, symbolized mathematically by the letter e, which is the variation in distance from the Sun as a fraction of the semi-major axis, but is often read as a percentage variation. |
According to Kepler's First Law of Planetary Motion, planetary orbits are ellipses with the Sun at one focus of the ellipse. This means that even if they have the same size, ellipses with different shapes do not have the same center. In the diagram below the focus of each ellipse is the same (for planetary orbits, the location of the Sun), but as the ellipse becomes more stretched out it also becomes more eccentric, meaning that the focus is further and further from the center of the ellipse. The eccentricity e is the fraction of the size of the ellipse which separates the focus from the center. For the ellipse with an eccentricity of zero the focus and the center are in the same place. An ellipse with an eccentricity of 0.40 has the focus 40% of the way from the center, in the direction of the periapsis -- the place (shown on the left in the diagram) where the ellipse is closest to the focus. Ellipses are also shown with eccentricities of 0.75 and 0.95, for which the focus is 75% and 95% of the way from the center to the periapsis point. For a planetary orbit this would put the planet 75% (or 95%) closer to the Sun at perihelion (the name used for the periapsis of an orbit around the Sun) than on the average, and 75% (or 95%) further from the Sun at aphelion (which is on the right side of the ellipses, as shown). (Note: Since all the orbits shown below have the same size and semi-major axis, the orbital periods would be the same; since the areas, perimeters and speeds of the objects following such different orbits would be different, this is a remarkable result.

None of the planets have orbits as elongated or eccentric as the examples above. The extreme example is Pluto, with an eccentricity of 0.25, which causes a 25% offset between the Sun and the center of the orbit; but its shape is almost identical to a circle which has the same center. As shown in the first diagram below, the eccentricity of its orbit causes Pluto to actually be closer to the Sun at perihelion than Neptune ever gets; but as shown in the following diagram, the shape of the orbit is actually almost circular, because the eccentricity is too small to cause large elongations such as those shown in the diagrams above. In the case of Pluto's orbit, even though the eccentricity is 0.25, the major axis is less than 1.6% longer, and the minor axis less than 1.6% shorter, than the radius of a circle of the same size and center (this means that its ellipticity is about 3.2%). As shown in the diagram below this would make the orbit appear to be very nearly circular, presuming that you could see the orbit (which you can't, since it is merely an imaginary curve).
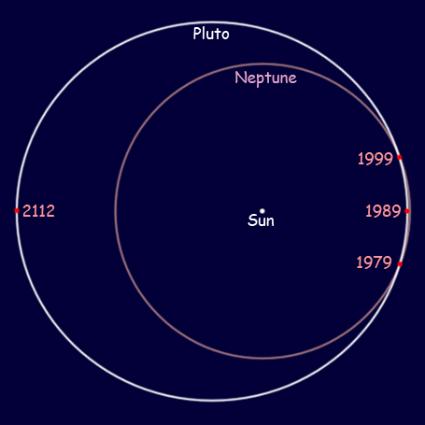
Pluto's orbit actually crosses Neptune's, in terms of distance from the Sun.

Although it has an eccentricity of 0.25, the shape of Pluto's orbit barely differs from that of a circle.
|